Following OpenGamma’s SIMM webinar – What you need to know about calculating SIMM – I wanted to add a little bit more colour regarding the Initial Margin of swaptions in the SIMM(R) framework.
In SIMM, the ‘S’ means standard. However, many people asked “how can this be for a liquid instrument like a swaption, when the numbers can be very different between counterparties?”
Yes, the ‘S’ in SIMM means Standard, but the standardisation is related to the computation of the Initial Margin based on sensitivities (Delta/Vega), not on the computation of the sensitivities. The sensitivities in SIMM are considered the inputs and not part of the methodology.
This variability of inputs is true for all models and all products. This is the case even for plain vanilla swaps where the sensitivities (bucketed PV01 or key rate durations) are strongly dependent on the interpolation mechanism. The high correlation between nodes in the risk weights/correlations approach selected for SIMM certainly lessens the impact on the Initial Margin, but it would already be present there.
So, I have decided to present the results for swaptions for several reasons.
- A personal reason: I’m an interest rate quant and I found my inspiration in that risk class when, almost 15 years ago, I wrote a paper titled ‘Swaptions: 1 Price, 10 Deltas, and… 6 1/2 Gammas’ (Henrard (2005) which was describing the same phenomenon that is at play here.
- A technical reason: The range of models used for swaption pricing is maybe larger than for other asset classes. With rates potentially going (or being) negative, the Black/log-normal model is not the only starting base. The models used for swaption pricing and risk management range from Black (1976) to Bachelier (1900) going through the very important SABR (Hagan et al. 2002). I could have added the Hull and White (1990) model, but in terms of delta the figures would have been almost equal to the Bachelier model.
SIMM and Models – Delta
How Does SIMM Work When The Users Adopt Different Models For The Valuation Of Their Derivatives?
For the delta, the inputs are sensitivities to the different vertices of the relevant yield curves. The sensitivities are the partial derivatives with respect to the market rates of outright swaps multiplied by one basis point (SIMM methodology V2.1, C.2.20). The practical meaning of partial derivatives is how the present value changes when the underlying changes. This is exactly what the model does; it explains how the present value of the derivative is impacted by the change of the underlying price. It is not surprising that the delta will be strongly dependent on the model.
The models I will use in this blog are the Bachelier, the Black and the SABR model. For SABR, there are a lot of potential parameterizations and I restricted myself to one with beta (the elasticity coefficient) equal to 0 and one with beta equal to 0.5. From historical data analysis presented in Henrard (2005), beta=0 is a reasonable choice in terms of delta hedging and beta=0.5 has been a popular choice in banks. With beta=0, the local volatility part of the SABR is similar to the Bachelier one and with beta=1 it is similar to the Black one.
For all the tests presented the following methodology was used: A realistic data set for USD curves and USD swaption prices, including smile, is used as a starting point. The SABR models are calibrated (with alpha, rho and nu parameters) at best to that set of data for each expiry and tenor considered. This is typically how the model would be used in practice. For each swaption considered, the implied Black volatility and implied Bachelier volatility are computed. We don’t use a grid of implied Black/Bachelier volatilities and interpolate in the grid but we recompute the implied volatility on the fly for each trade. There is no interpolation approximation for the comparison between models. The present value of each swaption considered is the same for all models. This is equivalent to the ‘one price’ part of the above mentioned article.
How Are The Deltas Different In Practice?
I will start with the example of long 1Yx5Y USD payer swaptions (standard conventions) for a notional of 1 million. I looked at two moneyness, one ATM and one OTM with a simple moneyness of +100 bps.
I will illustrate this using a couple of graphs first and will present more extensive tables later.
The total deltas (sum of bucketed deltas) are represented in Figure 1. Obviously with the delta larger for ATM than for OTM options and the left side of the figure as a different scale with larger numbers.
What is important for this analysis is that the deltas are significantly different between the models. The highest number (Black) is 23% higher than the lower (SABR 0). The relative difference is even higher for the out-of-the money option; the higher number is 77% higher than the lower one.
SIMM and Models – Vega
The issue of the diversity of the model is a little bit more complex for the vega. For SIMM purposes, the vega is defined as the partial derivative of the present value with respect to the implied volatility of the model. The SIMM language (paragraph C.3.30) indicates that for interest rate, the implied volatility can be “the normal volatility or log-normal volatility, or similar”. In all cases, the volatility changed is the ATM volatility “while keeping other inputs, including skew and smile constant”.
Our interpretation is that for Bachelier and Black we apply a shift of the implied volatility and for the SABR model, we apply a shift to the alpha parameter. Obviously, those different shifts will produce very different vegas, but the SIMM vega inputs computation does not stop there. The vega so computed is then multiplied by the implied volatility used (paragraph 8.10 (c) ). The vega is rescaled by the value of the number (volatility) on which it is based. This somewhat brings the numbers roughly in line; at least they are of the same dimension.
For the same options as in the previous section, we have computed those numbers in Figure 2. For the ATM example, all the rescaled vega are within 1% of each other. For the OTM case, the difference reaches almost 25%.
SIMM and Models – Initial Margin Results
From an Initial Margin perspective, the important thing is not the inputs but the output, i.e. the margin itself. The margin is composed of 3 parts, the delta Initial Margin, the vega Initial Margin and the curvature Initial Margin. The curvature Initial Margin is computed from the vega input using the relationship between gamma and vega in the Black model.
Once more we have used the same two examples to compute the Initial Margin. The results are presented in Figure 3. In the ATM example, the total IM is up to 15% higher in the most costly model (Black) than in the least costly one (SABR 0). In the OTM example, the total IM is up to 46% higher in the most costly model (Black) than in the least costly one (SABR 0).
Initial Margin Tables For Other Expiries, Tenors and Moneyness
The tables below highlight Initial Margin numbers for different expiries, tenors and moneyness. There are three tables, one with 1Yx5Y swaptions (as in the previous examples), one with 5Yx5Y swaptions and one with 10Yx10Y swaptions. For each of them we have listed five levels of moneyness, from -100bps to +100bps in 50bps steps.
Each table is divided into 4 parts; one for the Bachelier model, one for the Black model, one for SABR with CEV coefficient 0, and one for SABR with CEV coefficient 0.5. All the figures represent the IM computed with SIMM. The IM is divided, as per the SIMM methodology, between delta, vega and curvature.
If we look at the last table, for the 10Yx10Y swaptions, we see large discrepancies. For example for the swaption with a moneyness of 100 bps out of the money (above ATM), the delta IM varies between 5.25K and 20.25K, a ratio of almost 400%. The total IM is not showing such a ratio but still exhibits a ratio of 200%. This means that with the same market data and the same trade description, the IM can double dependent on the option model.
Conclusion
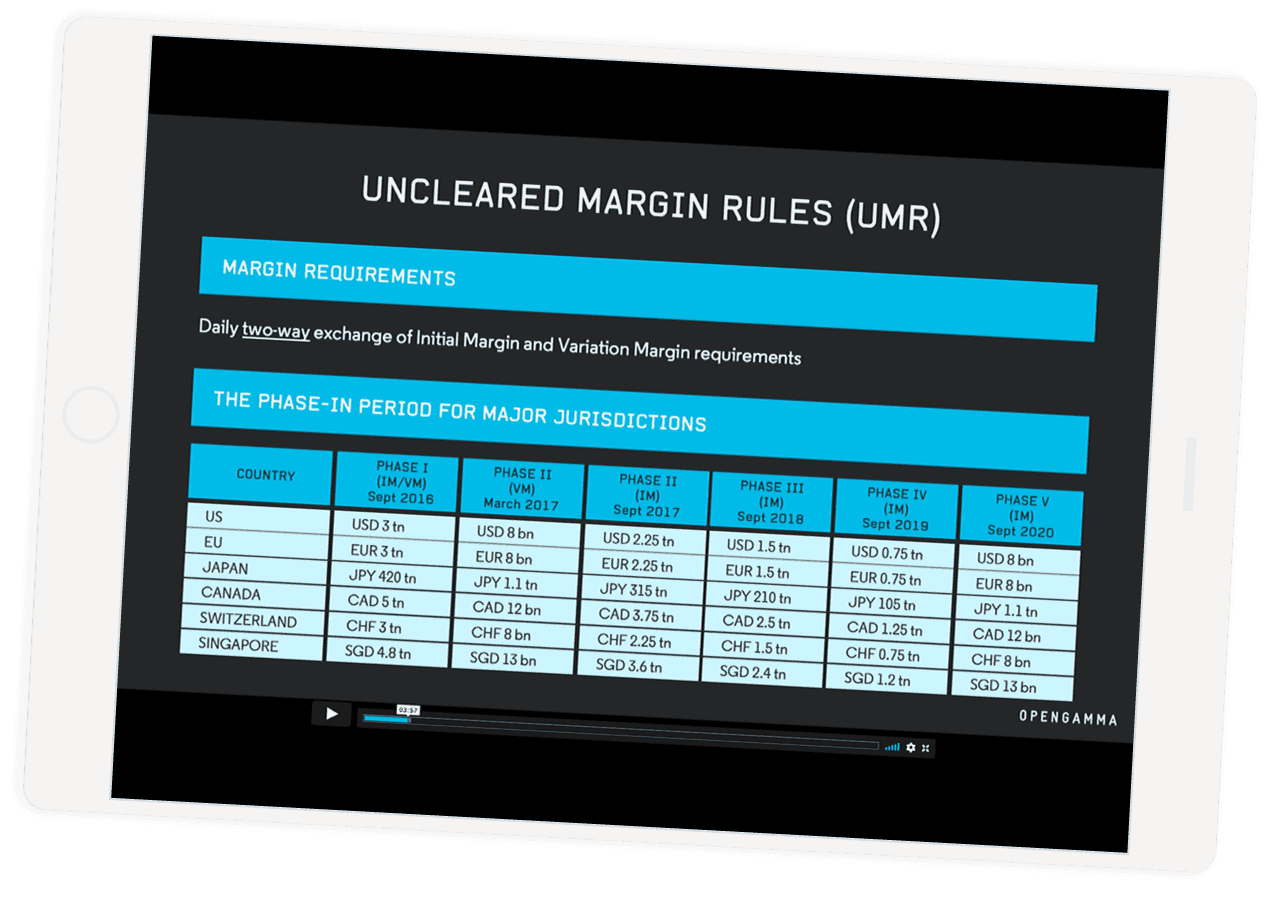
When calculating Initial Margin in relation to Uncleared Margin Rules (UMR), the most used methodology is the Standard Initial Margin Methodology (SIMM). The method is standard is the computation of Initial Margin from the trade sensitivities but the computation of the sensitivities is done by each counterparty according to its own methodology and not standardised.
In this note, using the example of vanilla swaptions and a set of standard models, we show that the resulting sensitivities and resulting Initial Margin can be very different, even for a single trade. There is no market wide standard that tells the market participants which one is better or which one should be used.
The SIMM figure reconciliation obviously require a back-office-like reconciliation of the trade population but also a quant-like reconciliation of the way the sensitivities are computed. It is almost impossible to understand the difference in Initial Margin figures between participants without an in-depth understanding of which method or model was used by each counterparty to generate the sensitivity. This excludes de facto any black-box approach or a process where the details of the model and its implementation are not available.
In our examples on swaptions, the Initial Margin numbers are in some cases more than doubled by changing the model used to compute sensitivities. The impact of those discrepancies are large enough to create cases where the posting counterparty believe that he is under the 50-million threshold but collecting party computations figures are above the threshold.
References
Bachelier, Louis (1900), Théorie de la Spéculation, PhD thesis from the Ecole Normale Supérieure.
Black, F. (1976). The pricing of commodity contracts. Journal of Financial Economics, 3(1-2):167-179.
P. Hagan, D. Kumar, A. Lesniewski, and D. Woodward. (2002) Managing smile risk. Wilmott Magazine, Sep:84-108, 2002.
Henrard, Marc (2005) Swaptions: One Price, 10 Deltas, and… 6 1/2 Gammas. Wilmott Magazine, pp. 48-57, November 2005